SLLists
In Chapter 2.1, we built the IntList class, a list data structure that can technically do all the things a list can do. However, in practice, the IntList suffers from the fact that it is fairly awkward to use, resulting in code that is hard to read and maintain.
Fundamentally, the issue is that the IntList is what I call a naked recursive data structure. In order to use an IntList correctly, the programmer must understand and utilize recursion even for simple list related tasks. This limits its usefulness to novice programmers, and potentially introduces a whole new class of tricky errors that programmers might run into, depending on what sort of helper methods are provided by the IntList class.
Inspired by our experience with the IntList, we'll now build a new class SLList, which much more closely resembles the list implementations that programmers use in modern languages. We'll do so by iteratively adding a sequence of improvements.
Improvement #1: Rebranding
Our IntList class from last time was as follows, with helper methods omitted:
public class IntList {
public int first;
public IntList rest;
public IntList(int f, IntList r) {
first = f;
rest = r;
}
...
Our first step will be to simply rename everything and throw away the helper methods. This probably doesn't seem like progress, but trust me, I'm a professional.
public class IntNode {
public int item;
public IntNode next;
public IntNode(int i, IntNode n) {
item = i;
next = n;
}
}
Improvement #2: Bureaucracy
Knowing that IntNodes are hard to work with, we're going to create a separate class called SLList that the user will interact with. The basic class is simply:
public class SLList {
public IntNode first;
public SLList(int x) {
first = new IntNode(x, null);
}
}
Already, we can get a vague sense of why a SLList is better. Compare the creation of an IntList of one item to the creation of a SLList of one item.
IntList L1 = new IntList(5, null);
SLList L2 = new SLList(5);
The SLList hides the detail that there exists a null link from the user. The SLList class isn't very useful yet, so let's add an addFirst and getFirst method as simple warmup methods. Consider trying to write them yourself before reading on.
addFirst and getFirst
addFirst is relatively straightforward if you understood chapter 2.1. With IntLists, we added to the front with the line of code L = new IntList(5, L). Thus, we end up with:
public class SLList {
public IntNode first;
public SLList(int x) {
first = new IntNode(x, null);
}
/** Adds an item to the front of the list. */
public void addFirst(int x) {
first = new IntNode(x, first);
}
}
getFirst is even easier. We simply return first.item:
/** Retrieves the front item from the list. */
public int getFirst() {
return first.item;
}
The resulting SLList class is much easier to use. Compare:
SLList L = new SLList(15);
L.addFirst(10);
L.addFirst(5);
int x = L.getFirst();
to the IntList equivalent:
IntList L = new IntList(15, null);
L = new IntList(10, L);
L = new IntList(5, L);
int x = L.first;
Comparing the two data structures visually, we have:
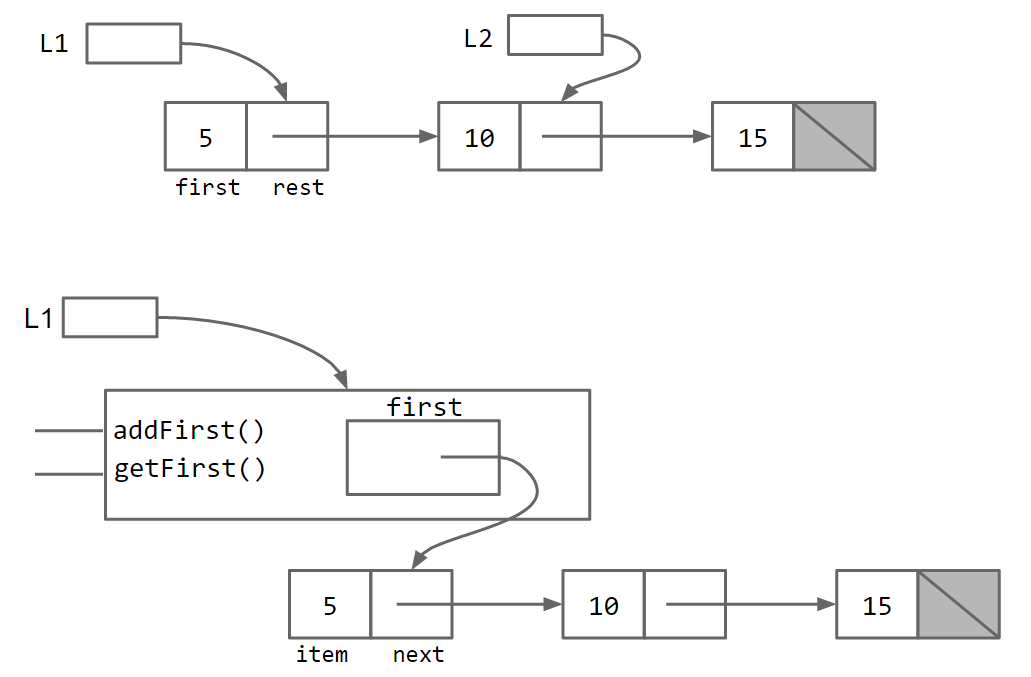
Essentially, the SLList class acts as a middleman between the list user and the naked recursive data structure. As Ovid said:
Mortals cannot look upon a god without dying, so perhaps it is best that the SLList is there to act as our intermediary.
Exercise 2.2.1: The curious reader might object and say that the IntList would be just as easy to use if we simply wrote an addFirst method. Try to write an addFirst method to the IntList class. You'll find that the resulting method is tricky as well as inefficient.
Improvement #3: Public vs. Private
Unfortunately, our SLList can be bypassed and the raw power of our naked data structure (with all its dangers) can be accessed. A programmer can easily modify the list directly, without going through the kid-tested, mother-approved addFirst method, for example:
SLList L = new SLList(15);
L.addFirst(10);
L.first.next.next = L.first.next;
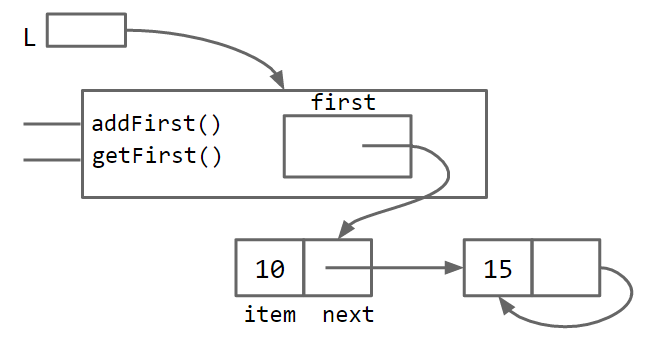
This results in a malformed list with an infinite loop. To deal with this problem, we can modify the SLList class so that the first variable is declared with the private keyword.
public class SLList {
private IntNode first;
...
Private variables and methods can only be accessed by code inside the same .java file, e.g. in this case SLList.java. That means that a class like SLLTroubleMaker below will fail to compile, yielding a first has private access in SLList error.
public class SLLTroubleMaker {
public static void main(String[] args) {
SLList L = new SLList(15);
L.addFirst(10);
L.first.next.next = L.first.next;
}
}
By contrast, any code inside the SLList.java file will be able to access the first variable.
It may seem a little silly to restrict access. After all, the only thing that the private keyword does is break programs that otherwise compile. However, in large software engineering projects, the private keyword is an invaluable signal that certain pieces of code should be ignored (and thus need not be understood) by the end user. Likewise, the public keyword should be thought of as a declaration that a method is available and will work forever exactly as it does now.
As an analogy, a car has certain public features, e.g. the accelerator and brake pedals. Under the hood, there are private details about how these operate. In a gas powered car, the accelerator pedal might control some sort of fuel injection system, and in a battery powered car, it may adjust the amount of battery power being delivered to the motor. While the private details may vary from car to car, we expect the same behavior from all accelerator pedals. Changing these would cause great consternation from users, and quite possibly terrible accidents.
When you create a public member (i.e. method or variable), be careful, because you're effectively committing to supporting that member's behavior exactly as it is now, forever.
Improvement #4: Nested Classes
At the moment, we have two .java files: IntNode and SLList. However, the IntNode is really just a supporting character in the story of SLList.
Java provides us with the ability to embed a class declaration inside of another for just this situation. The syntax is straightforward and intuitive:
public class SLList {
public class IntNode {
public int item;
public IntNode next;
public IntNode(int i, IntNode n) {
item = i;
next = n;
}
}
private IntNode first;
public SLList(int x) {
first = new IntNode(x, null);
}
...
Having a nested class has no meaningful effect on code performance, and is simply a tool for keeping code organized. For more on nested classes, see Oracle's official documentation.
If the nested class has no need to use any of the instance methods or variables of SLList, you may declare the nested class static, as follows. Declaring a nested class as static means that methods inside the static class can not access any of the members of the enclosing class. In this case, it means that no method in IntNode would be able to access first, addFirst, or getFirst.
public class SLList {
public static class IntNode {
public int item;
public IntNode next;
public IntNode(int i, IntNode n) {
item = i;
next = n;
}
}
private IntNode first;
...
This saves a bit of memory, because each IntNode no longer needs to keep track of how to access its enclosing SLList.
Put another way, if you examine the code above, you'll see that the IntNode class never uses the first variable of SLList, nor any of SLList's methods. As a result, we can use the static keyword, which means the IntNode class doesn't get a reference to its boss, saving us a small amount of memory.
If this seems a bit technical and hard to follow, try Exercise 2.2.2. A simple rule of thumb is that if you don't use any instance members of the outer class, make the nested class static.
Exercise 2.2.2 Delete the word static as few times as possible so that this program compiles. Make sure to read the comments at the top before doing the exercise.
addLast() and size()
To motivate our remaining improvements and also demonstrate some common patterns in data structure implementation, we'll add addLast(int x) and size() methods. You're encouraged to take the starter code and try it yourself before reading on. I especially encourage you to try to write a recursive implementation of size, which will yield an interesting challenge.
I'll implement the addLast method iteratively, though you could also do it recursively. The idea is fairly straightforward, we create a pointer variable p and have it iterate through the list to the end.
/** Adds an item to the end of the list. */
public void addLast(int x) {
IntNode p = first;
/* Advance p to the end of the list. */
while (p.next != null) {
p = p.next;
}
p.next = new IntNode(x, null);
}
By contrast, I'll implement size recursively. This method will be somewhat similar to the size method we implemented in section 2.1 for IntList.
The recursive call for size in IntList was straightforward: return 1 + this.rest.size(). For a SLList, this approach does not make sense. A SLList has no rest variable. Instead, we'll use a common pattern that is used with middleman classes like SLList -- we'll create a private helper method that interacts with the underlying naked recursive data structure.
This yields a method like the following:
/** Returns the size of the list starting at IntNode p. */
private static int size(IntNode p) {
if (p.next == null) {
return 1;
}
return 1 + size(p.next);
}
Using this method, we can easily compute the size of the entire list:
public int size() {
return size(first);
}
Here, we have two methods, both named size. This is allowed in Java, since they have different parameters. We say that two methods with the same name but different signatures are overloaded. For more on overloaded methods, see Java's official documentation.
An alternate approach is to create a non-static helper method in the IntNode class itself. Either approach is fine, though I personally prefer not having any methods in the IntNode class.
Improvement #5: Caching
Consider the size method we wrote above. Suppose size takes 2 seconds on a list of size 1,000. We expect that on a list of size 1,000,000, the size method will take 2,000 seconds, since the computer has to step through 1,000 times as many items in the list to reach the end. Having a size method that is very slow for large lists is unacceptable, since we can do better.
It is possible to rewrite size so that it takes the same amount of time, no matter how large the list.
To do so, we can simply add a size variable to the SLList class that tracks the current size, yielding the code below. This practice of saving important data to speed up retrieval is sometimes known as caching.
public class SLList {
... /* IntNode declaration omitted. */
private IntNode first;
private int size;
public SLList(int x) {
first = new IntNode(x, null);
size = 1;
}
public void addFirst(int x) {
first = new IntNode(x, first);
size += 1;
}
public int size() {
return size;
}
...
}
This modification makes our size method incredibly fast, no matter how large the list. Of course, it will also slow down our addFirst and addLast methods, and also increase the memory of usage of our class, but only by a trivial amount. In this case, the tradeoff is clearly in favor of creating a cache for size.
Improvement #6: The Empty List
Our SLList has a number of benefits over the simple IntList from chapter 2.1:
- Users of a
SLListnever see theIntListclass.- Simpler to use.
- More efficient
addFirstmethod (exercise 2.2.1). - Avoids errors or malfeasance by
IntListusers.
- Faster
sizemethod than possible withIntList.
Another natural advantage is that we will be able to easily implement a constructor that creates an empty list. The most natural way is to set first to null if the list is empty. This yields the constructor below:
public SLList() {
first = null;
size = 0;
}
Unfortunately, this causes our addLast method to crash if we insert into an empty list. Since first is null, the attempt to access p.next in while (p.next != null) below causes a null pointer exception.
public void addLast(int x) {
size += 1;
IntNode p = first;
while (p.next != null) {
p = p.next;
}
p.next = new IntNode(x, null);
}
Exercise 2.2.2: Fix the addLast method. Starter code here.
Improvement #6b: Sentinel Nodes
One solution to fix addLast is to create a special case for the empty list, as shown below:
public void addLast(int x) {
size += 1;
if (first == null) {
first = new IntNode(x, null);
return;
}
IntNode p = first;
while (p.next != null) {
p = p.next;
}
p.next = new IntNode(x, null);
}
This solution works, but special case code like that shown above should be avoided when necessary. Human beings only have so much working memory, and thus we want to keep complexity under control wherever possible. For a simple data structure like the SLList, the number of special cases is small. More complicated data structures like trees can get much, much uglier.
A cleaner, though less obvious solution, is to make it so that all SLLists are the "same", even if they are empty. We can do this by creating a special node that is always there, which we will call a sentinel node. The sentinel node will hold a value, which we won't care about.
For example, the empty list created by SLList L = new SLList() would be as shown below:
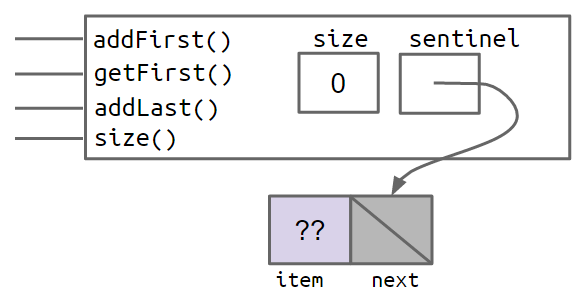
And a SLList with the items 5, 10, and 15 would look like:
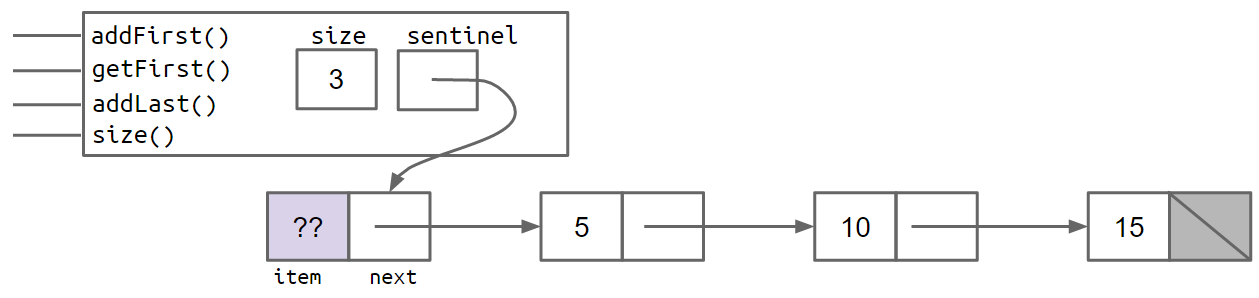
In the figures above, the lavender ?? value indicates that we don't care what value is there. Since Java does not allow us to fill in an integer with question marks, we just pick some abitrary value like -518273 or 63 or anything else.
Since a SLList without a sentinel has no special cases, we can simply delete the special case from our addLast method, yielding:
public void addLast(int x) {
size += 1;
IntNode p = sentinel;
while (p.next != null) {
p = p.next;
}
p.next = new IntNode(x, null);
}
As you can see, this code is much much cleaner!
Invariants
An invariant is a fact about a data structure that is guaranteed to be true (assuming there are no bugs in your code).
A SLList with a sentinel node has at least the following invariants:
- The
sentinelreference always points to a sentinel node. - The front item (if it exists), is always at
sentinel.next.item.- The
sizevariable is always the total number of items that have been added.
- The
Invariants make it easier to reason about code, and also give you specific goals to strive for in making sure your code works.
A true understanding of how convenient sentinels are will require you to really dig in and do some implementation of your own. You'll get plenty of practice in project 1. However, I recommend that you wait until after you've finished the next section of this book before beginning project 1.
What Next
Nothing for this chapter. However, if you're taking the Berkeley course, you're welcome to now begin Lab 2.