Trees and Traversals
What is a tree?
Recall that a tree consists of:
- A set of nodes (or vertices). We use both terms interchangeably.
- A set of edges that connect those nodes.
- Constraint: There is exactly one path between any two nodes.

The left-most structure is a tree. It has a node. It has no edges. That's OK!
The second and third structures are trees.
The fourth is not a tree. Why? There are two paths from the top node to the bottom node, and so this does not obey our constraint.
Exercise 17.1.1. Determine the reason why the fifth structure is not a tree. Also, modify the invalid trees above so that they are valid.
What is a rooted tree?
Recall that a rooted tree is a tree with a designated root (typically drawn as the top most node.)
This gives us the notion of two more definitions
- A parent. Every node except the root has exactly one parent.
- What if a node had 2 parents? Would it be a tree? (Hint: No.)
- A child. A node can have 0 or more children.
- What if a node has 0 children? It's called a leaf.
What are trees useful for?
So far, we've looked at Search Trees, Tries, Heaps, Disjoint Sets, etc. These were extremely useful in our journey to create efficient algorithms: speeding up searching for items, allowing prefixing, checking connectedness, and so on.
But the fact of the matter is that they are even more ubiquitous than we realize. Consider an organization chart. Here, the President is the 'root'. The 'VP's are children of the root, and so on.
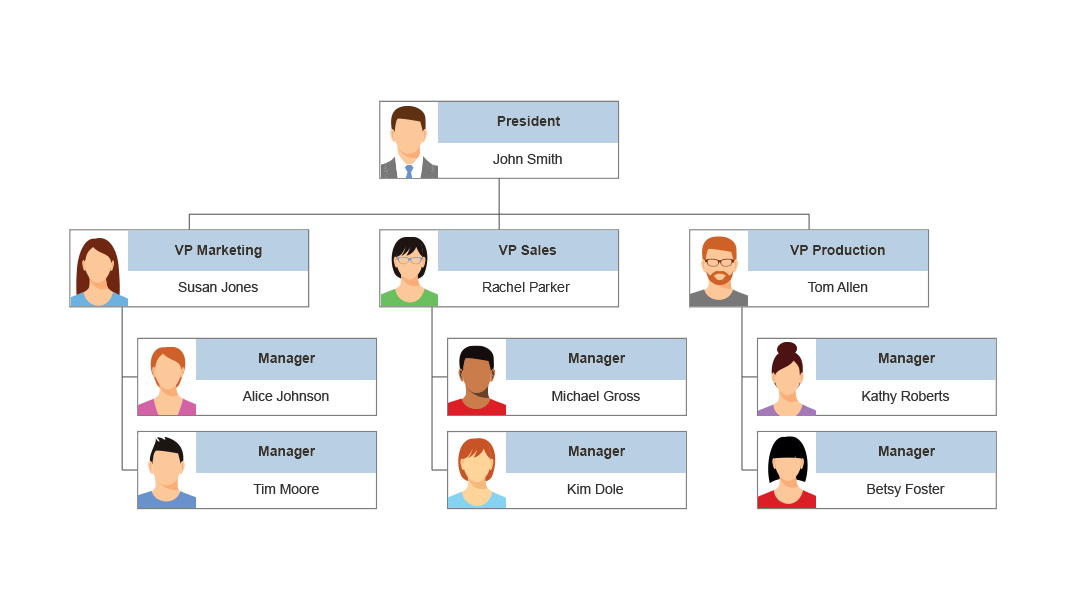
Another tree structure is the 61b/ directory on your Desktop (it is on your Desktop, isn't it?). As we can see, when you traverse to a subfolder it goes to subsequent subfolders and so on. This is exactly tree-like!

Exercise 17.1.2. Think of other common uses of trees that weren't mentioned above. Try and determine possible implementations or designs of these trees.