Topological Sort

We have covered a tremendous amount of material so far. Programming practices, using an IDE, designing data structures, asymptotic analysis, implementing a ton of different abstract data types (e.g. using a BST, Trie, or HashTable to implement a map, heaps to implement a Priority Queue), and finally algorithms on graphs.

Why is this knowledge useful?

You may have heard people say that CS 61B teaches much of what you need to solve standard interview questions at tech companies - but why do companies seek candidates with this specific knowledge?

One major reason is that many real world problems can be formulated in such a way that they're solvable with the data structures and algorithms we've learned. This chapter is about working through some tricky problems using the tools we have already learned.

Topological Sorting

Suppose we have a collection of different tasks or activities, some of which must happen before another. How do we find sort the tasks such that for each task $v$, the tasks that happen before $v$ come earlier in our sort?

We can first view our collection of tasks as a graph in which each node represents a task. An edge $v \rightarrow w$ indicates that $v$ must happen before $w$. Now our original problem is reduced to finding a topological sort.

Topological Sort: an ordering of a graph's vertices such that for every directed edge $u \rightarrow v$, $u$ comes before $v$ in the ordering.

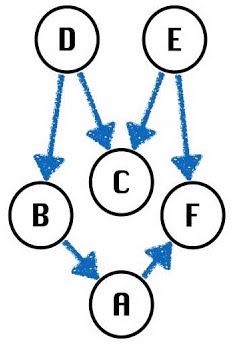
Question 1.1: What are some valid topological orderings of the above graph?

Answer: Valid orderings include: $[D, B, A, E, C, F]$, $[E, D, C, B, A, F]$.

An important note is that it only makes sense to topological sort certain types of graphs. To see this, consider the following graph:

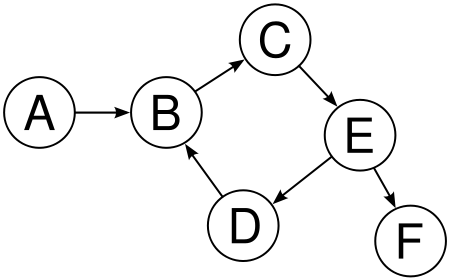
What is a valid topological sorting of this?

There isn't one! D comes before B but B comes before C, E, D. Since we have a cycle, topological sort is not defined. We also can't topologically sort an undirected graph since each edge in an undirected graph creates a cycle.

So topological sorts only apply to directed, acyclic (no cycles) graphs - or DAGs.

Topological Sort: an ordering of a DAG's vertices such that for every directed edge $u \rightarrow v$, $u$ comes before $v$ in the ordering.

For any topological ordering, you can redraw the graph so that the vertices are all in one line. Thus, topological sort is sometimes called a linearization of the graph. For example, here's the earlier example linearized for one of the topological orderings.

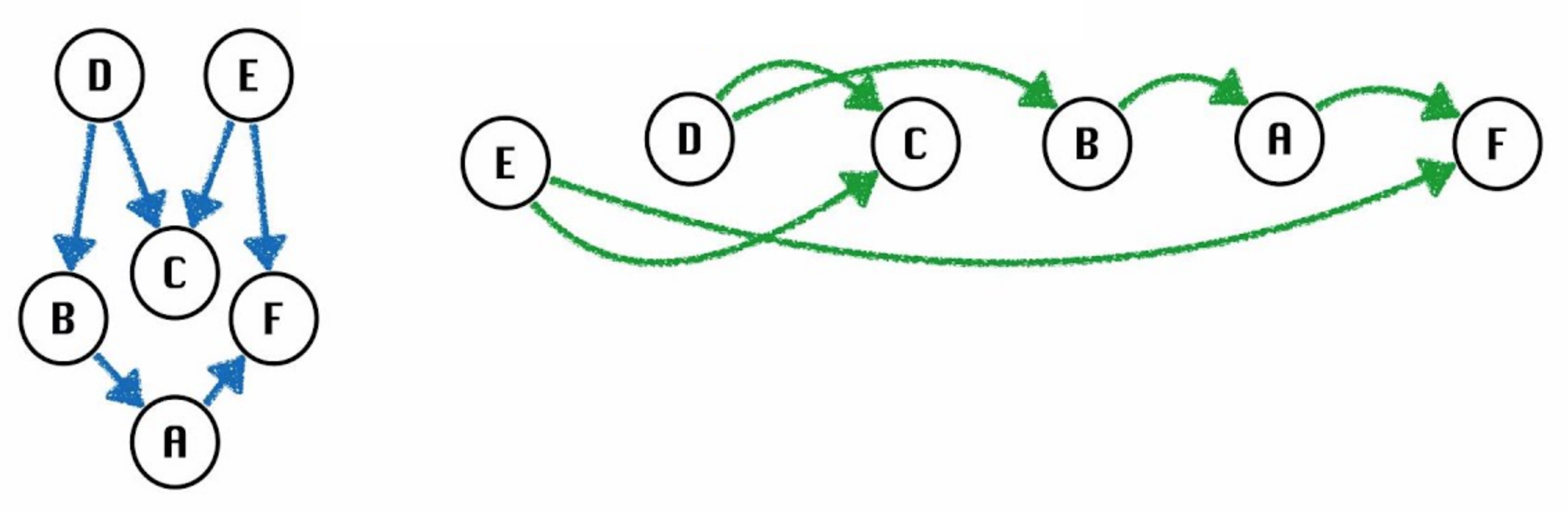
Notice that the topological sort for the above DAG has to start with either D or E and must end with F or C. For this reason, D and E are called sources, and F and C are called sinks.

Topological Sort Algorithm

How can we find a topological sort? Take a moment to think of existing graph algorithms you already know could be helpful in solving this problem.

Topological Sort Algorithm:

• Perform a DFS traversal from every vertex in the graph, not clearing markings in between traversals.
• Record DFS postorder along the way.
• Topological ordering is the reverse of the postorder.

Why it works: Each vertex $v$ gets added to the end of the postorder list only after considering all descendants of $v$. Thus, when any $v$ is added to the postorder list, all its descendants are already on the list. Thus reversing this list gives a topological ordering.

Since we're simply using DFS, the runtime of this is $O(V + E)$ where $V$ and $E$ are the number of nodes and edges in the graph respectively.

Pseudocode

topological(DAG):
    initialize marked array
    initialize postOrder list
    for all vertices in DAG:
        if vertex is not marked:
            dfs(vertex, marked, postOrder)
    return postOrder reversed

dfs(vertex, marked, postOrder):
    marked[vertex] = true
    for neighbor of vertex:
        dfs(neighbor, marked, postOrder)
    postOrder.add(vertex)

(Out of scope) Extra question: How could we implement topological sort using BFS? Hint 1: We'd definitely need to store some extra information. Hint 2: Think about keeping track of the in-degrees of each vertex.

Solution:

1. Calculate in-degree of all vertices.
2. Pick any vertex $v$ which has in-degree of 0.
3. Add $v$ to our topological sort list. Remove the vertex $v$ and all edges coming out of it. Decrement in-degrees of all neighbors of vertex $v$ by 1.
4. Repeat steps 2 and 3 until all vertices are removed.

How can we accomplish Step 2 efficiently? We can use a min Priority Queue of vertices with priority equal to the in-degrees.

Review

• Topological sorts are a way of linearizing Directed, Acyclic Graphs (DAGs).
• We can find a topological sort of any DAG in $O(V + E)$ time using DFS (or BFS).