Weighted Quick Union (WQU)
Improving on Quick Union relies on a key insight: whenever we call find, we have to climb to the root of a tree. Thus, the shorter the tree the faster it takes!
New rule: whenever we call connect, we always link the root of the smaller tree to the larger tree.
Following this rule will give your trees a maximum height of , where N is the number of elements in our Disjoint Sets. How does this affect the runtime of connect and isConnected?
Let's illustrate the benefit of this with an example. Consider connecting the two sets T1 and T2 below:
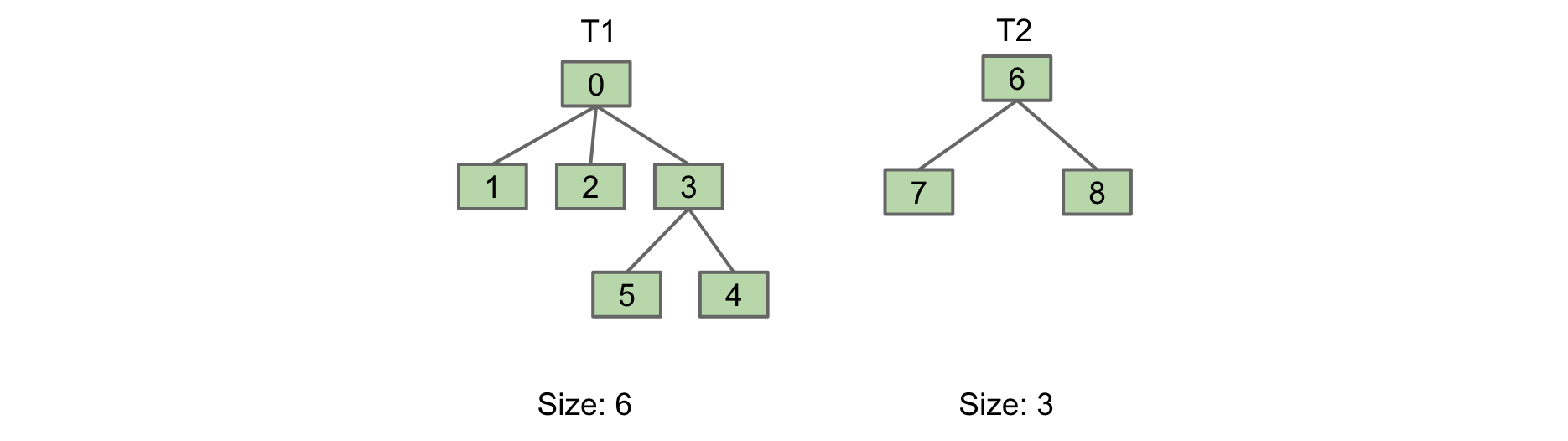
We have two options for connecting them:
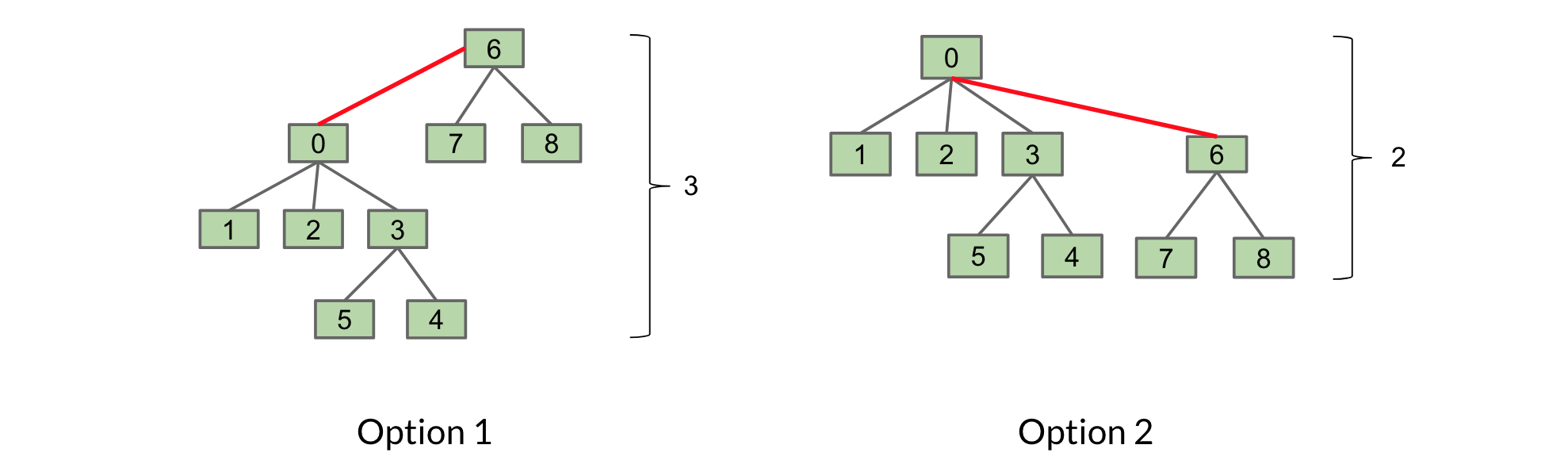 The first option we link T1 to T2. In the second, we link T2 to T1.
The first option we link T1 to T2. In the second, we link T2 to T1.
The second option is preferable as it only has a height of 2, rather than 3. By our new rule, we would choose the second option as well because T2 is smaller than T1 (size of 3 compared to 6).
We determine smaller / larger by the number of items in a tree. Thus, when connecting two trees we need to know their size (or weight). We can store this information in the root of the tree by replacing the -1's with -(size of tree). You will implement this in Lab 6.
Maximum height: Log N
Following the above rule ensures that the maximum height of any tree is Θ(log N). N is the number of elements in our Disjoint Sets. By extension, the runtimes of connect and isConnected are bounded by O(log N).
Why log N? The video above presents a more visual explanation. Here's an optional mathematical explanation why the maximum height is . Imagine any element in tree . The depth of increases by only when is placed below another tree . When that happens, the size of the resulting tree will be at least double the size of because . The tree with can double at most times until we've reached a total of N items (). So we can double up to times and each time, our tree adds a level maximum levels.
You may be wondering why we don't link trees based off of height instead of weight. It turns out this is more complicated to implement and gives us the same Θ(log N) height limit.
Summary and Code
| Implementation | Constructor | connect |
isConnected |
|---|---|---|---|
| QuickUnion | Θ(N) | O(N) | O(N) |
| QuickFind | Θ(N) | Θ(N) | Θ(1) |
| QuickUnion | Θ(N) | O(N) | O(N) |
| Weighted Quick Union | Θ(N) | O(log N) | O(log N) |
N = number of elements in our DisjointSets data structure
Code? That's your Lab 6!