Reductions

Recall in previous section that to solve one problem (longest paths), we created a new graph G' and fed it into a different algorithm and then interpreted the result.

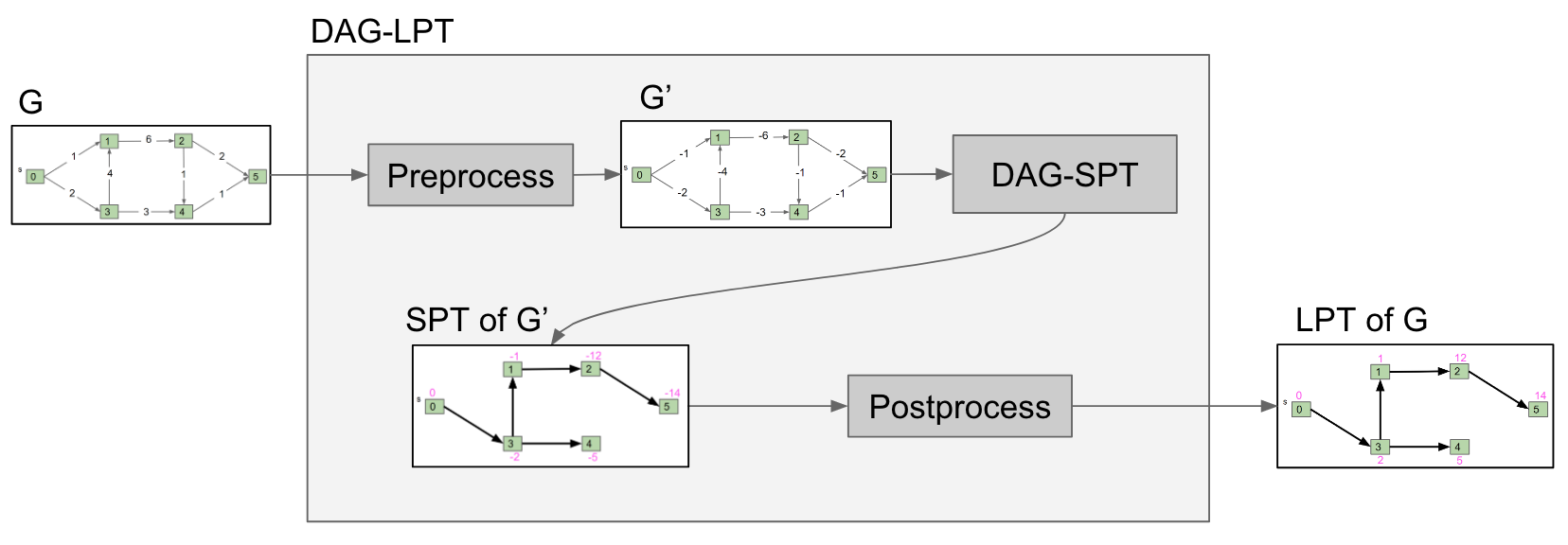
This process is known as reduction. Since DAG-SPT can be used to solve DAG-LPT, we say that "DAG-LPT reduces to DAG-SPT."

In other words, the problem of DAG-LPT can be reduced to the problem of DAG-SPT.

A problem like DAG-LPT can potentially be reduced to multiple other problems. As a real-world analogy, consider climbing a hill. There are many ways we can solve the problem of "climbing a hill."

• "Climbing a hill" reduces to "riding a ski lift"
• "Climbing a hill" reduces to "being shot out of a cannon"
• "Climbing a hill" reduces to "riding a bike up the hill"

Formally, if any subroutine for task Q can be used to solve P, we say P reduces to Q.

This definition is visualized below:

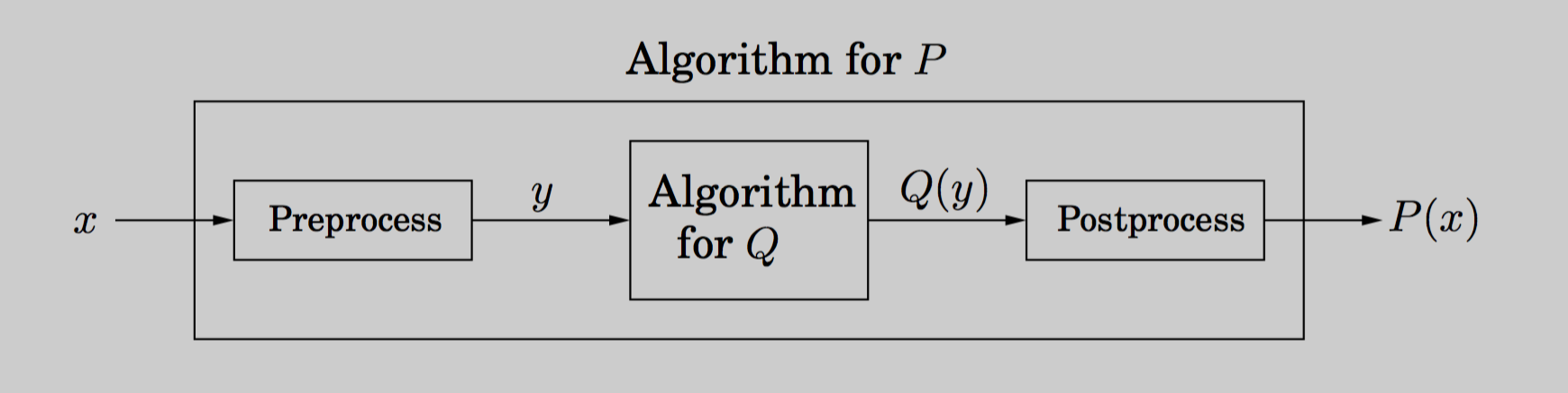
Note that this is simply a generalization of the first graphic on this page. P reduces to Q since Q is used to solve P. This works by preprocessing the input $x$ into $y$, running the algorithm Q on $y$, and postprocessing the output into a solution for P. This is what we did for reducing DAG-LPT to DAG-SPT.

Example

Here we'll show how one problem can reduce to a seemingly unrelated different problem. First, the two problems:

Independent Set Problem

An independent set is a set of vertices in which no two vertices are adjacent.

The Independent Set Problem: Does there exist an independent set of size k? In other words, can we color k vertices red, such that none touch?

Example of independent sets solutions for k=2 and k=4

3SAT Problem

What values of x1, x2, x3, x4 satisfy the following boolean formula: (x1 || x2 || !x3) && (x1 || !x1 || x1) && (x2 || x3 || x4)?

The 3SAT Problem: Given a boolean formula, does there exist a truth value for boolean variables that obeys a set of 3-variable disjunctive constraints?

Terminology clarification:

• Constraints are True/False values.
• Disjunctive means separated by OR. 3SAT has a set of "clauses," each made up of 3 literals with each literal separated by an OR. For example, the first clause above is (x1 || x2 || !x3).
• In the 3SAT problem we must satisfy the entire set of clauses (combine each clause with AND).

e.g.: (x1 || x2 || !x3) && (x1 || !x1 || x1) && (x2 || x3 || x4)       Yes, a solution for x1, x2, x3, x4 exists       Solution: x1 = true, x2 = true, x3 = true, x4 = false

Reduction

CLAIM: 3SAT reduces to Independent Set

• Recall this means we claim we can solve 3SAT by using the Independent Set algorithm!

PROOF: To prove the reduction, we need to argue that we can:

1. Preprocess a given 3SAT problem
2. Solve it with Independent Set
3. Postprocess the output of part 2 into a solution to the original 3SAT problem.

Let's do it!

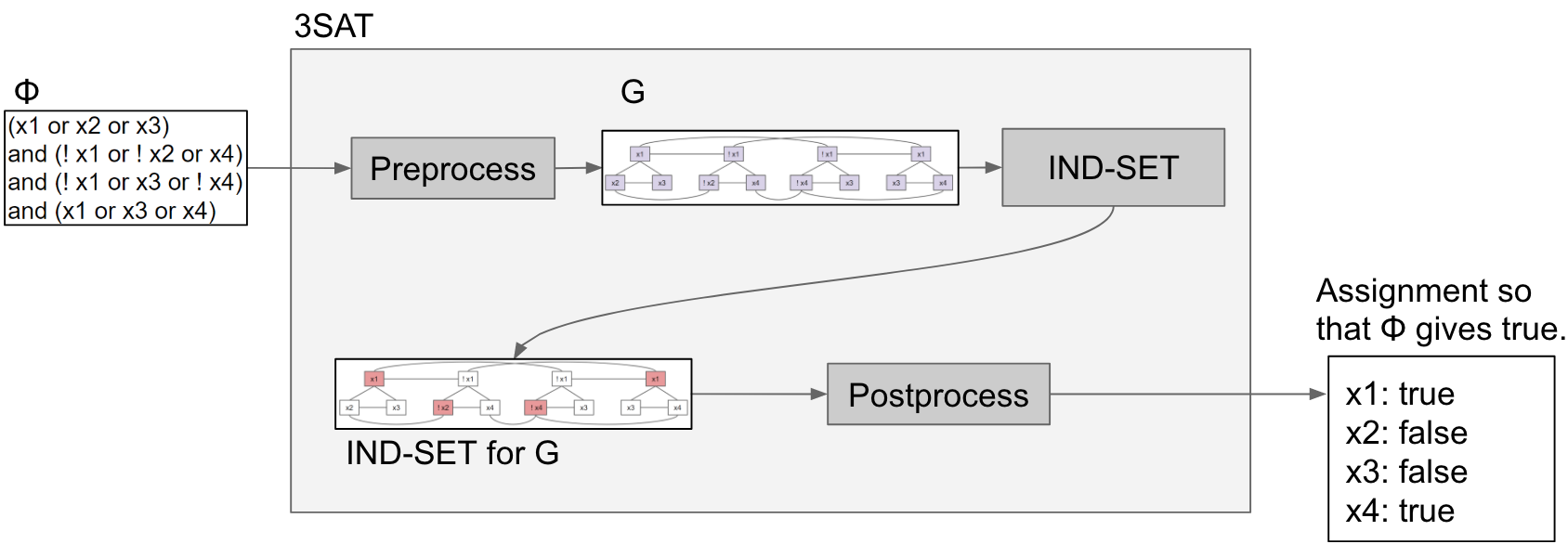
Preprocess a given 3SAT problem Given an instance X of 3SAT, preprocess it into a graph G:

1. For each clause in X, create 3 vertices in a triangle
2. Add an edge between each literal and its negation

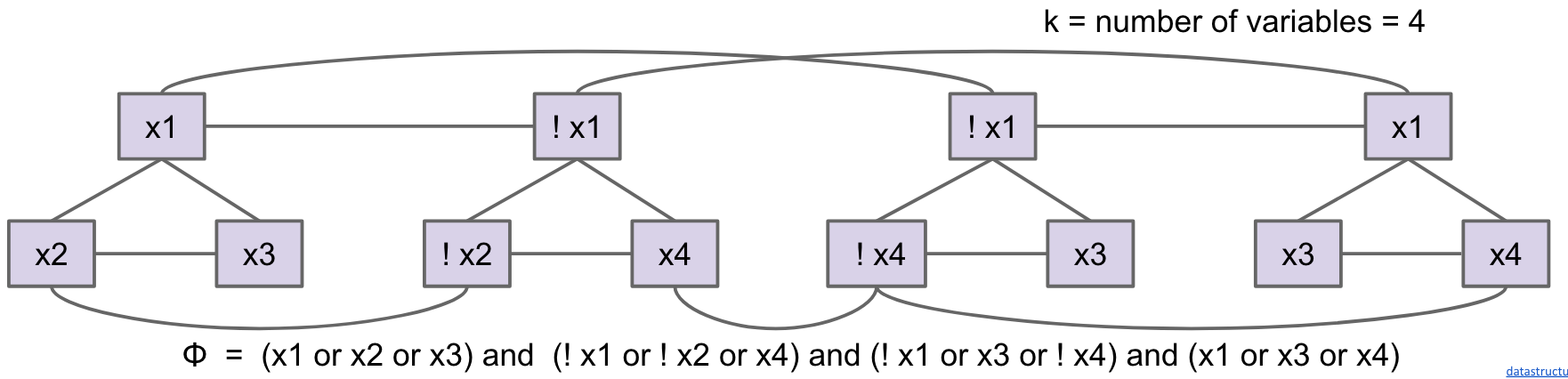
Solve with Independent Sets On graph G, find an independent set of size = number of clauses in 3SAT.

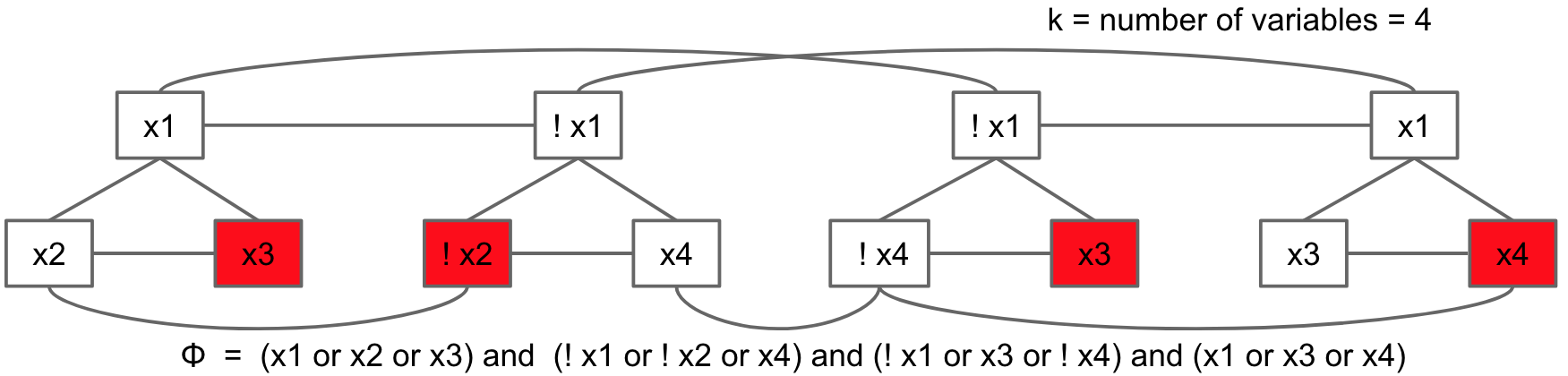
Postprocess the output Elements in the independent set are considered "True", while elements outside are considered "False." If you can find an independent set of size = number of clauses in 3SAT, then you've successfully solved 3SAT (using independent sets whoo!).

In the above example, since x3, !x2, x3, x4 were picked for the independent set, we consider each of those literals to be True and values for the rest don't matter. Therefore, x3 = True, x2 = False, x4 = True, x1 = doesn't matter.

Why this works: We'll reference the below example when going through the proof.

(x1 || x2 || !x3) && (x1 || !x1 || x1) && (x2 || x3 || x4)

The above 3SAT problem has 3 clauses. To form a satisfying truth assignment we must pick one literal from each clause and give it the value True. Of course, we must be consistent. If we choose x1 to be True in the first clause, we can't choose !x1 to be True in the third clause (x1 can't both be True and False!).

Representing a clause by a triangle forces us to pick only literal in a clause for the independent set. Repeat this for every clause and and finding an independent set of size = number of clauses means exactly one literal will be picked from each clause (we'll consider a picked node to be True).

We also make sure to add an edge from each literal to its negation to prevent us from choosing opposite literals (e.g. both x1 and !x1) in different clauses. This may also have the effect of finding an independent set impossible - in this case, 3SAT is also not solvable.

Here's a visualization of the above reduction:

Note that reductions are a general concept and apply to many different types of problems (they don't always involve creating graphs!)

Reflection

One can argue that we have been doing reduction all throughout the course.

• Abstract Lists reduce to arrays or linked lists
• Percolation reduces to Disjoint Sets
• Maze generation reduces to [your solution here ;)]

However these aren't exactly reductions because you aren't using a single other algorithm to solve your problem. Notably, in the earlier reduction example we used the Independent Sets algorithm as a 'black box' to solve 3SAT.

Perhaps a better term for what we've been accomplishing earlier in the course is decomposition - breaking a complex task into smaller parts. Using abstraction to make problem solving easier. This is the heart of computer science.