Omega and Amortized Analysis
In this section, we'll wrap up our discussion of asymptotics. Much of this material won't be expanded on until later in the course. This section expands on the concept of Big O and introduces Omega. We'll also explore the idea of amortized runtimes and their analysis. Finally, we'll end on empirical analysis of runtimes and a sneak preview of complexity theory.
Runtime Analysis Subtleties
To demonstrate why it is useful to use Big O, let's go back to our duplicate-finding functions consider the following exercises.
Exercise: Let be the runtime of dup3 as a function of N, the length of the array. What is the order of growth of ?
public boolean dup3(int[] a) {
int N = a.length;
for (int i = 0; i < N; i += 1) {
for (int j = 0; j < N; j += 1) {
if (a[i] == a[j]) {
return true;
}
}
}
return false;
}
Answer: , it's constant time! That's because there's a bug in dup3: it always compares the first element with itself. In the very first iteration, i and j are both 0, so the function always immediately returns. Bummer!
Let's fix up the bug in dup4 and try it again.
Exercise: Let be the runtime of dup4 as a function of N, the length of the array. What is the order of growth of ?
public boolean dup4(int[] a) {
int N = a.length;
for (int i = 0; i < N; i += 1) {
for (int j = i + 1; j < N; j += 1) {
if (a[i] == a[j]) {
return true;
}
}
}
return false;
}
Answer: This time, the runtime depends on not only the length of the input, but also the array's contents. In the best case, . If the input array contains all of the same element, then no matter how long it is, dup4 will return on the first iteration.
On the other hand, in the worst case, . If the array has no duplicates, then dup4 will never return early, and the nested for loop will result in quadratic runtime.
This exercise highlights one limitation of Big Theta. Big Theta expresses the exact order of as a function of the input size. However, if the runtime depends on more than just the size of the input, then we must qualify our statements into different cases before using Big Theta. Big O does away with this annoyance. Rather than having to describe both the best and worse case, for the example above, we can simply say that the runtime of dup4 is . Sometimes dup4 is faster, but it's at worst quadratic.
Big O Abuse
Consider the following statements:
- The most expensive room in the hotel is $639 per night.
- Every room in the hotel is less than or equal to $639 per night.
Which statement gives you more information about a hotel?
The first one. The second statement provides only an upper bound on room prices, ie. an inequality. The first statement tells you not only the upper bound of room prices, but also that this upper bound is reached. For example, consider a cheap hotel whose most expensive room is $89/night and an expensive one whose most expensive room is $639/night. Both hotels fulfill the second statement, but the first statement narrows it down to just the latter hotel.
Exercise: Which statement gives you more information about the runtime of a piece of code?
- The worst case runtime is Θ(N^2).
- The runtime is O(N^2). Answer: Similar to the hotel problem, the first statement provides more information. Consider the following method:
public static void printLength(int[] a) {
System.out.println(a.length);
}
Both this simple method and dup4 have runtime , so knowing statement 2 would not be able to distinguish between these. But statement 1 is more precise, and is only true for dup4.
In the real world, and oftentimes in conversation, Big O is often used where in places where Big Theta would be more informative. We saw one good reason for this -- it frees us from needing to use qualifying statements. However, while the looser statement is true, it's not as useful as a Big Theta bound.
Note: Big O is NOT the same as "worst case". But it is often used as such.
To summarize the usefulness of Big O:
- It allows us to make simple statements without case qualifications, in cases where the runtime is different for different inputs.
- Sometimes, for particularly tricky problems, we (the computer science community) don't know the exact runtime, so we may only state an upper bound.
- It's a lot easier to write proofs for Big O than Big Theta, like we saw in finding the runtime of mergesort in the previous chapter. This is beyond the scope of this course.
Big Omega
To round out our understanding of runtimes, let's also define the complement of Big O, to describe lower bounds.
While Big Theta can be informally thought of as runtime equality and Big O represents "less than or equal", Big Omega can be thought of as the "greater than or equal". For example, in addition to knowing that , all of the following statements are true:
If , then the function is also "greater than or equal to" . The function must also grow faster than any function slower asymptotically than , eg. and .
There's two common uses for Big Omega:
- It's used to prove Big Theta runtime. If and , then . Sometimes, it's easier to prove O and separately. This is outside the scope of this course.
- It's used to prove the difficulty of a problem. For example, ANY duplicate-finding algorithm must be , because the algorithm must at least look at each element.
Here's a table to summarize the three Big letters:
| Informal Meaning | Example Family | Example Family Members | |
|---|---|---|---|
| Big Theta | Order of growth is f(N) | ||
| Big O | Order of growth is less than or equal to f(N) | ||
| Big Omega | Order of growth is greater than or equal to f(N) |
Amortized Analysis (Intuitive Explanation)
Grigometh's Urn
Grigometh is a demon dog that looks a bit spooky. He offers you the ability to appear to horses in their dreams, just like how he sometimes appears in your dreams and midterms. However, in return for this ability, you must periodically offer him urnfuls of hay, as tribute. He gives you two payment options:
- Choice 1: Every day, Grigometh eats 3 bushels of hay from your urn.
- Choice 2: Grigometh eats exponentially more hay over time, but comes exponentially less frequently. Specifically:
- On day 1, he eats 1 bushel of hay (total 1)
- On day 2, he eats 2 additional bushels of hay (total 3)
- On day 4, he eats 4 additional bushels of hay (total 7)
- On day 8, he eats 8 additional bushels of hay (total 15)
You want to develop a routine and put a fixed amount of hay in your urn each day. How much hay must you put in the earn each day for each payment scheme? Which is cheaper?
For the first choice, you'd have to put exactly 3 bushels of hay in the urn each day. However, the second choice actually turns out to be a a bit cheaper! You can get away with just putting in 2 bushels of hay in the urn each day. (Try to convince yourself why this is true -- one way to do this is the write out the total amount of hay you contribute after each day. You'll notice that whenever Grigometh comes for his hay snack, you'll always have one extra bushel in the urn after he takes his fill. Neat.)
Bushels aside, notice here that Grigometh's hay consumption per day is effectively constant, and in choice 2, we can describe this situation as amortized constant hay consumption.
AList Resizing and Amortization
It turns out, Grigometh's hay dilemma is very similar to AList resizing from early in the course. Recall that in our implementation of array-based lists, when we call the add method on an AList whose underlying array is full, we need to resize the array. In other words, the add method, when full, must create a new array of larger size, copy over the old elements, and then finally add the new element. How much bigger should our new array be? Recall the following two implementations:
Implementation 1
public void addLast(int x) {
if (size == items.length) {
resize(size + RFACTOR);
}
items[size] = x;
size += 1;
}
Implementation 2
public void addLast(int x) {
if (size == items.length) {
resize(size * RFACTOR);
}
items[size] = x;
size += 1;
}
The first implementation turned out to be unusably bad. When our array fills up, every time a new element is added, the entire array must be copied to a new one. The second implementation, which we called geometric resizing, on the other hand, worked nicely. In fact, this is how Python lists are implemented.
Let's look into the runtime of implementation 2 in more detail. Let RFACTOR be 2. When the array is full, resize doubles its size. Most add operations take time, but some are very expensive, and linear to the current size. However, if we average out the cost of expensive adds with resize over all the adds that are cheap, and given that expensive adds with happen half as frequently every time it happens, it turns out that on average, the runtime of add is . We'll prove this in the next section. In the meantime, here's a graph to illustrate this:
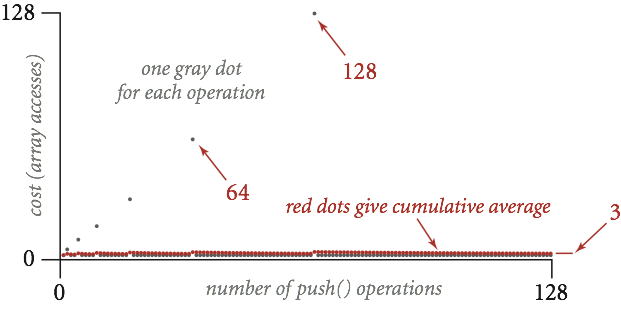
Amortized Analysis (Rigorous Explanation)
A more rigorous examination of amortized analysis is done here, in three steps:
- Pick a cost model (like in regular runtime analysis)
- Compute the average cost of the i'th operation
- Show that this average (amortized) cost is bounded by a constant.
Suppose that initially, our ArrayList contains a length-1 array. Let's apply these three steps to ArrayList resizing:
- For our cost model, we'll only consider array reads and writes. (You could also include other operations into your cost model, such as array creation and the cost of filling in default array values. But it turns out that these will all yield the same result.)
- Let's compute the cost of a sequence of array adds. Suppose we had the following code and accompanying diagram:
TODO: image
- x.add(0) performs 1 write operation. No resizing. Total: 1 operation
- x.add(1) resizes and copies the existing array (1 read, 1 write), and then writes the new element. Total: 3 operations
- x.add(2) resizes and copies the existing array (2 reads, 2 writes), and then writes the new element. Total: 5 operations
- x.add(3) does not resize, and only writes the new element. Total: 1 operations
- x.add(4) resizes and copies the existing array (4 reads, 4 writes), and then writes the new element. Total: 9 operations
It's easier to keep track of this in a table:
| Insert # | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a[i] write cost | 1 | 1 | 1 | 1 | 1 | |||||||||
| Resize/copy cost | 0 | 2 | 4 | 0 | 8 | |||||||||
| Total cost for # | 1 | 3 | 5 | 1 | 9 | |||||||||
| Cumulative cost | 1 | 4 | 9 | 10 | 19 |
Exercise: Fill out the rest of this table. Total cost is the total cost for one particular insert. Cumulative cost is the cost for all inserts so far.
Answer:
| Insert # | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a[i] write cost | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| Resize/copy cost | 0 | 2 | 4 | 0 | 8 | 0 | 0 | 0 | 16 | 0 | 0 | 0 | 0 | 0 |
| Total cost for # | 1 | 3 | 5 | 1 | 9 | 1 | 1 | 1 | 17 | 1 | 1 | 1 | 1 | 1 |
| Cumulative cost | 1 | 4 | 9 | 10 | 19 | 20 | 21 | 22 | 39 | 40 | 41 | 42 | 43 | 44 |
So what is the average cost of the a sequence of adds? For 13 adds, this average cost is per add. But for the first 8 adds, the average cost is per add.
- Is the average (amortized) cost bounded by a constant? It seems like it might be bounded by 5. But just by looking at the first 13 adds, we cannot be completely sure.
We'll now introduce the idea of "potential" to aid us in solving this amortization mystery. For each operation i, eg. each add or Grigometh visit, let be the true cost of the operation, while be some arbitrary amortized cost of the operation. , a constant, must be the same for all i.
Let be the potential at operation i, which is the cumulative difference between amortized and true cost:
is an arbitrary constant, meaning we can chose it. If we chose such that is never negative and is constant for all , then the amortized cost is an upper bound on the true cost. And if the true cost is upper bounded by a constant, then we've shown that it is on average constant time!
Let's try this for Grigometh's hay tribute. For each day i, the actual cost is how much hay Grigometh eats on that day. The amortized cost is how much hay we put in the urn on that day -- let's assume that's 3. Let the initial potential be :
| Day (i) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Actual cost | 1 | 2 | 0 | 4 | 0 | 0 | 0 | 0 | 8 | 0 | 0 | 0 | 0 | 0 |
| Amortized cost | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 |
| Change in potential | 2 | 1 | 3 | -1 | 3 | 3 | 3 | 3 | -5 | 3 | 3 | 3 | 3 | 3 |
| Potential | 2 | 3 | 6 | 5 | 8 | 11 | 14 | 17 | 12 | 15 | 18 | 21 | 24 | 27 |
If we let , the potential never falls negative -- in fact, it looks like after many days, we will keep on having a surplus of hay for Grigometh, if we add 3 bushels per day. We'll save the rigorous proof of this for another course, but hopefully the trend looks convincing enough. So Grigometh's hay tribute is on average constant.
Exercise: We'd like to conserve as much hay as possible. Show that we can satisfy Grigometh's hunger and never have negative potential even if we set .
Now back to ArrayList resizing.
Exercise: What is the value of for ArrayList add operations? If we let the amortized cost , will the potential ever become negative? Is there a smaller amortized cost that works? Fill out a table like the one for Grigometh to help with this.
Answer: is the total cost for array resizing and adding the new element, where if i is a power of 2, and otherwise.
| Insert # | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Actual cost | 1 | 3 | 5 | 1 | 9 | 1 | 1 | 1 | 17 | 1 | 1 | 1 | 1 | 1 |
| Amortized cost | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 |
| Change in potential | 4 | 2 | 0 | 4 | -4 | 4 | 4 | 4 | -12 | 4 | 4 | 4 | 4 | 4 |
| Potential | 4 | 6 | 6 | 10 | 6 | 10 | 14 | 18 | 6 | 10 | 14 | 18 | 22 | 26 |
By looking at the trend, the potential should never be negative (proof for this is omitted). Intuitively, for high-cost operations, we use the previous low-cost operations to store up potential.
Finally, we've shown that ArrayList add operations are indeed amortized constant time. Geometric resizing (multiplying by the RFACTOR) leads to good list performance.
Summary
- Big O is an upper bound ("less than or equals")
- Big Omega is a lower bound ("greater than or equals")
- Big Theta is both an upper and lower bound ("equals")
- Big O does NOT mean "worst case". We can still describe worst cases using Big Theta
- Big Omega does NOT mean "best case". We can still describe best cases using Big Theta
- Big O is sometimes colloquially used in cases where Big Theta would provide a more precise statement
- Amortized analysis provides a way to prove the average cost of operations.
- If we chose such that is never negative and is constant for all , then the amortized cost is an upper bound on the true cost.